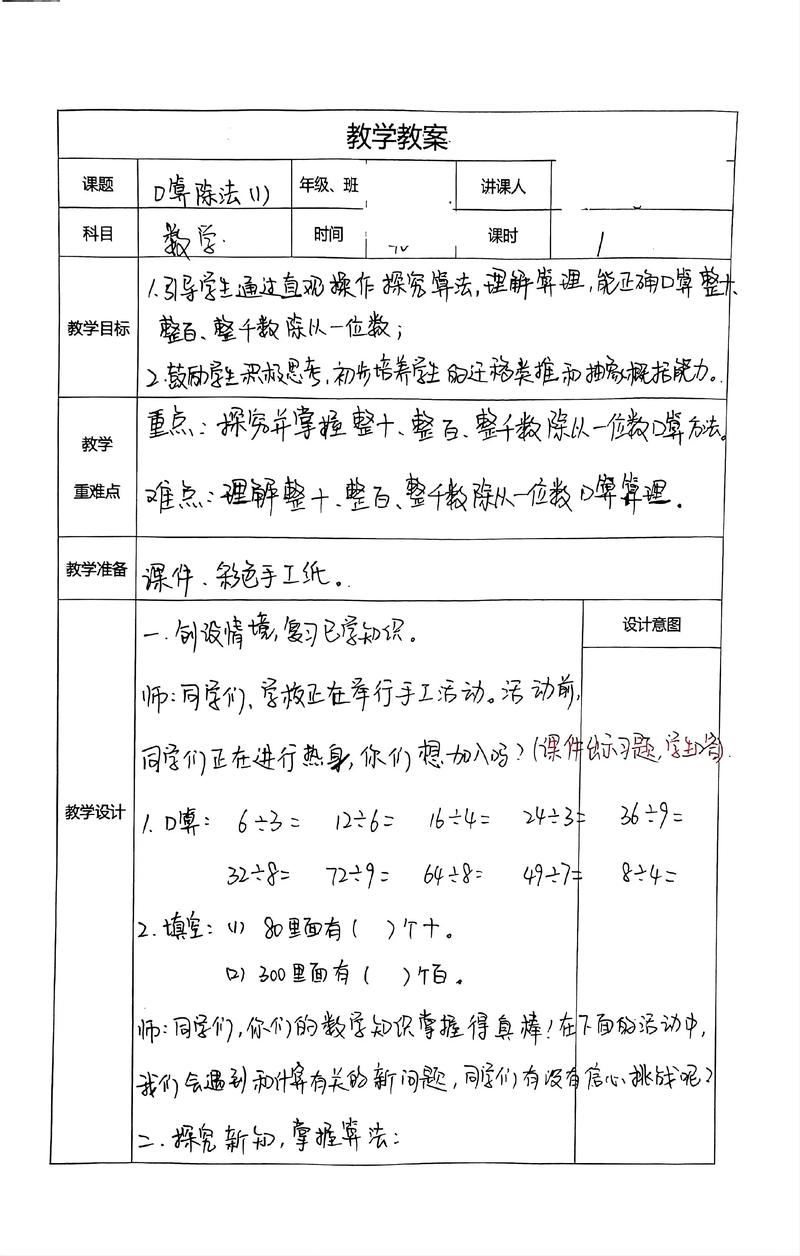
小学数学三年级下册《两位数乘两位数(不进位)》教案
教学基本信息
- 课题: 两位数乘两位数(不进位)
- 教材版本: 人民教育出版社(人教版)三年级下册
- 课时: 第1课时
- 授课对象: 三年级学生
- 执教教师: [教师姓名]
教学目标
-
知识与技能目标:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 使学生理解并掌握两位数乘两位数(不进位)的竖式计算方法,并能正确进行计算。
- 理解竖式计算中每一步所表示的实际意义,即“部分积”的含义。
-
过程与方法目标:
- 引导学生通过情境问题、动手操作、合作探究等方式,经历从口算、笔算到竖式计算的抽象过程,培养其迁移类推和抽象概括的能力。
- 在解决问题的过程中,体验算法的多样化,并学会优化选择最适合自己的方法。
-
情感态度与价值观目标:
- 感受数学与生活的密切联系,体验用数学知识解决实际问题的乐趣。
- 培养认真、细致的计算习惯和初步的逻辑思维能力。
教学重难点
-
教学重点: 掌握两位数乘两位数(不进位)的竖式计算方法,并能正确计算。
-
教学难点: 理解两位数乘两位数竖式计算中“对位”的道理,即第二个部分积的末位为什么要与十位对齐。
 (图片来源网络,侵删)
(图片来源网络,侵删)
教学准备
- 教师准备: 多媒体课件(PPT)、磁性小棒或小方块、板书设计稿。
- 学生准备: 练习本、铅笔、直尺。
教学过程
(一) 创设情境,导入新课 (约5分钟)
-
情境引入:
- PPT展示情境图:王老师要去书店买一批新书,每套14元,她买了12套,请问王老师一共需要付多少钱?
- 引导学生列出算式:
14 × 12。
-
复习旧知,迁移铺垫:
- 提问:同学们,我们以前学过哪些乘法计算方法?(口算、一位数乘两位数)
- 引导学生尝试口算:
14 × 12可以怎么算?- 方法一(拆分法):
14 × 10 = 140,14 × 2 = 28,140 + 28 = 168。 - 方法二(交换位置):
12 × 14,10 × 14 = 140,2 × 14 = 28,140 + 28 = 168。
- 方法一(拆分法):
- 教师肯定学生的想法,并提问:当数字变大时,口算是不是就有点麻烦了?有没有一种更规范、更通用的计算方法呢?从而引出课题——两位数乘两位数的笔算。
(二) 探究新知,理解算理 (约15分钟)
(图片来源网络,侵删)
-
直观操作,理解分步计算:
- 提问:
14 × 12表示什么意思?(12个14相加) - 我们可以把12拆成10和2,那么计算就分成了两步。
- 第一步:计算 2 个 14 是多少。
- 提问:我们先算哪个部分?(
14 × 2) - 请学生用小棒摆一摆:1捆(10根)和4根,这样的2份是多少?(2捆和8根,是28)
- 板书:
14 × 2 = 28,这个“28”表示2套书的价格,是28元。
- 提问:我们先算哪个部分?(
- 第二步:计算 10 个 14 是多少。
- 提问:再算哪个部分?(
14 × 10) - 提问:为什么这里不是算
14 × 1,而是14 × 10?(因为这里是10个14,不是1个14) - 引导学生思考:
14 × 10得多少?(140) - 板书:
14 × 10 = 140,这个“140”表示10套书的价格,是140元。
- 提问:再算哪个部分?(
- 第三步:将两部分合起来。
- 提问:最后要做什么?(把两部分价格加起来)
- 板书:
140 + 28 = 168。 14 × 12 = 168。
- 提问:
-
抽象过渡,学习竖式计算:
- 教师引导:刚才我们用分步计算的方法解决了问题,这个过程其实和竖式计算的道理是一样的,我们把这个过程“竖”起来写,就是竖式。
- 教师示范竖式写法,并讲解每一步:
1 4 <-- 第一个因数 × 1 2 <-- 第二个因数 ------ 2 8 <-- 第一步:14 × 2 = 28,这是2个14,所以个位对齐,我们称之为“部分积”。 1 4 <-- 第二步:14 × 1 = 14,这是1个“十”,所以4要写在十位上,这个“14”代表的是140。 ------ 1 6 8 <-- 第三步:将两个部分积相加,得到最终结果。 - 突破难点(对位问题):
- 教师用彩色粉笔或PPT高亮显示第二个部分积“14”末尾的“4”。
- 关键提问: “同学们看,这里的‘4’为什么要写在十位上,而不是和上面的‘8’对齐呢?”
- 引导学生结合分步计算回答:因为它代表的是
14 × 10,是140,个位的0可以省略不写,但计算时我们要记住它是在十位上的。 - 再次强调:第二个部分积的末位,一定要与第二个因数的十位对齐!
-
小组讨论,总结算法:
- 请学生以小组为单位,讨论并总结两位数乘两位数(不进位)竖式计算的步骤。
- 教师引导学生归纳,并板书计算法则:
- 相同数位对齐。
- 用第二个因数的个位去乘第一个因数,积的末位和个位对齐。
- 用第二个因数的十位去乘第一个因数,积的末位和十位对齐。
- 把两次乘得的积加起来。
(三) 巩固练习,深化理解 (约15分钟)
-
基础练习(“做一做”):
- PPT出示教材例题后的“做一做”题目。
23 × 13 =33 × 11 =43 × 12 =- 请3名学生上台板演,其他学生在练习本上独立完成。
- 集体订正,重点关注竖式格式和对位是否正确,对出错的学生进行个别指导。
-
改错练习(火眼金睛):
- PPT出示几个有典型错误的竖式计算。
- 错误1:对位错误。
- 错误2:忘记加部分积。
- 错误3:乘法口诀记错。
- 请学生当“小医生”,找出错误并说明原因,然后改正,通过辨析,加深对算理的理解。
- PPT出示几个有典型错误的竖式计算。
-
解决问题(学以致用):
- 一个篮球32元,体育老师买了11个,一共需要多少钱?
- 引导学生先列式,再用竖式计算,并写出答语,培养学生解决问题的完整能力。
(四) 课堂总结,回顾提升 (约5分钟)
-
回顾知识:
- 提问:这节课我们学习了什么?(两位数乘两位数)
- 提问:计算时要注意什么?(相同数位对齐,第二个部分积的末位要和十位对齐)
- 提问:为什么第二个部分积的末位要和十位对齐?(因为它表示的是几十,是乘以10的结果)
-
分享收获:
- 请学生分享自己在本节课的收获或困惑。
- 教师总结:今天我们不仅学会了计算,更重要的是理解了计算背后的道理,希望同学们在今后的计算中,都能做到“知其然,并知其所以然”。
板书设计
一个好的板书是课堂教学的“微型教案”,应简洁、重点突出、条理清晰。
| 两位数乘两位数(不进位) |
|---|
| 情境问题: 买12套书,每套14元,一共多少钱? |
算式: 14 × 12 = ? |
| 分步计算: |
14 × 2 = 28 (2套的钱) |
14 × 10 = 140 (10套的钱) |
28 + 140 = 168 (总钱数) |
| 竖式计算: |
| ``` |
| 1 4 |
| × 1 2 |
| ------ |
| 2 8 ← 14 × 2 的积 (个位对齐) |
| 1 4 ← 14 × 1 的积 (十位对齐,代表140) |
| ------ |
| 1 6 8 |
| ``` |
| 计算法则: |
| 相同数位对齐。 |
| 用第二个因数的个位乘,积的末位对个位。 |
| 用第二个因数的十位乘,积的末位对十位。 |
| 把两次的积相加。 |
| 答:一共需要168元。 |
教学反思
本节课的设计力求体现以学生为主体的教学理念。
-
成功之处:
- 情境导入有效: 从学生熟悉的生活情境入手,自然地引出数学问题,激发了学生的学习兴趣。
- 算理讲解透彻: 通过“分步计算”作为桥梁,将抽象的竖式计算与学生的已有知识和直观经验(小棒)联系起来,特别是针对“对位”这一难点,设计了关键提问,引导学生自己说出原因,突破了教学难点。
- 练习设计有层次: 从基础的模仿练习,到改错的辨析练习,再到解决问题的应用练习,层层递进,符合学生的认知规律,确保了知识的巩固和内化。
-
改进之处:
- 时间分配: 在探究新知环节,学生动手操作和小组讨论的时间可能需要更精确地控制,避免影响后续练习的充分性。
- 关注个体差异: 对于理解能力稍弱的学生,可能在课堂巡视中需要给予更多、更具体的个别指导,例如再次用小棒演示“14 × 10”为什么是140。
- 拓展延伸: 可以在总结后,简单提问:“如果题目变成
14 × 22,也就是个位相乘需要进位,那又该怎么算呢?”为下一节课的学习埋下伏笔,激发学生的持续探究欲望。


